Nella parte 1, abbiamo sfidato il modo consueto di valutare l'errore assoluto medio semplicemente prendendo la differenza tra la media prevista e il risultato osservato. Abbiamo scoperto che è necessario utilizzare il corretto stimatore puntuale, la mediana, per riassumere la distribuzione per un singolo numero, in linea con l'interpretazione operativa dell'Errore Assoluto. Ciò comporta, tuttavia, alcune proprietà sgradevoli del MAE: è a grana grossa, discontinuo e inutile per chi si muove lentamente.
Completa il palcoscenico per il punteggio di probabilità classificato
Chiaramente, la situazione con cui vi ho lasciato nella prima parte di questo post non è soddisfacente: il MAE è discontinuo, impreciso e persino inutile per i lenti con medie previste inferiori a 0,69. Ciononostante, la sua ragionevole interpretazione commerciale – il costo è proporzionale all'errore – rimane attraente. Possiamo risolverlo?
Potremmo semplicemente abbandonare la mediana e usare qualche altro riassunto, come il mezzo molto più benevolo? Sfortunatamente, fingere che la distinzione mediana/media sia irrilevante non la rende tale. Seguire questa strada non risolve i nostri problemi, ma ne introduce di nuovi: la previsione che vincerebbe a un MAE valutato in modo errato sarebbe distorta.
Quali sono allora le nostre possibilità di migliorare l'AE, dato che siamo legati alla mediana come riassunto? C'è un aspetto che possiamo cambiare, ovvero l'ordine dei due processi "riassumere" e "calcolare l'errore". Attualmente, prima riassumiamo (distribuzione mappata allo stimatore di punti) e poi calcoliamo l'errore ("stimatore di punti - risultato"). Facciamo un respiro profondo e scambiamo i due passaggi, come illustrato nel grafico sottostante (lato sinistro): Data una distribuzione prevista (rosso) e un risultato osservato (blu), calcoliamo l'AE per ogni risultato previsto (frecce nere):
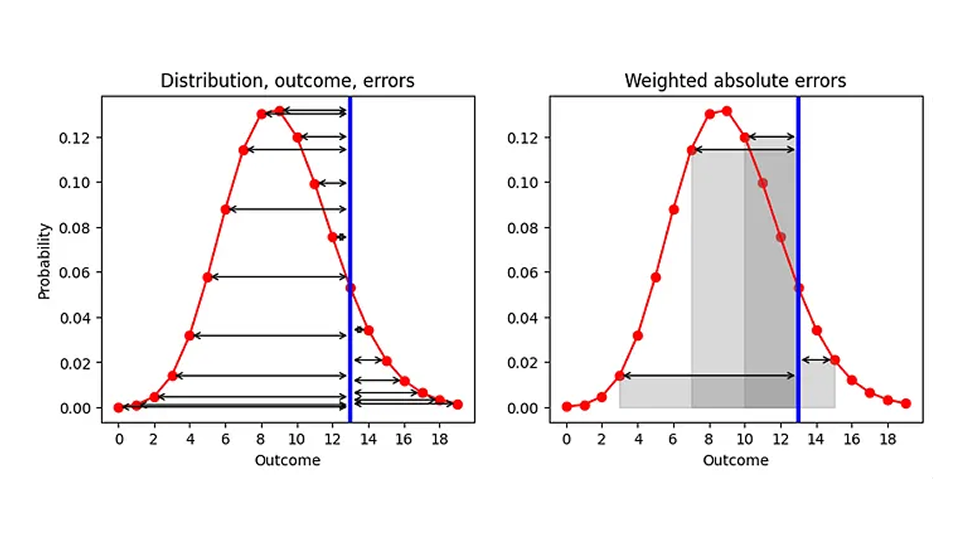
Il risultato è un elenco di eventi avversi, uno per ogni risultato (incluso il pronostico che corrisponde al risultato effettivo, per il quale l'evento avverso è 0). Poiché il nostro obiettivo è quello di sostituire AE, un singolo numero, dobbiamo riassumere questi numerosi AE. Prendiamo la media degli eventi avversi, con la probabilità che avevamo assegnato a ciascun risultato come peso in quella media. Geometricamente, stiamo sommando le aree racchiuse tra le frecce di errore e l'asse x, come illustrato per alcuni risultati nel grafico a destra.
Questa prescrizione è una definizione ragionevole per la distanza tra un numero e una distribuzione di probabilità: si pesa ogni distanza verso un possibile risultato in base alla probabilità assegnata a quel risultato. Come caso limite, se la distribuzione fosse 0 ovunque tranne che per un risultato, per il quale è 1 (una previsione deterministica che prevede che questo risultato si realizzerà sicuramente), recuperiamo l'AE tradizionale: il valore assoluto della distanza tra quel risultato previsto deterministicamente e l'osservazione. Il nostro AE migliorato diventa l'AE tradizionale per le previsioni deterministiche!
Possiamo esprimere la prescrizione attraverso questa formula:
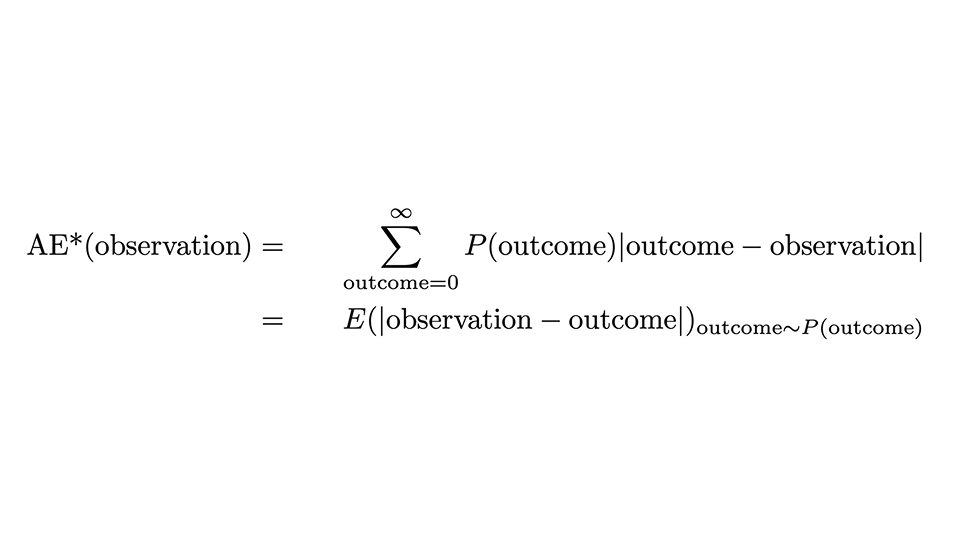
Sembra un po' spaventoso, ma esaminiamolo delicatamente: l'AE*, l'"AE corretto", per un'osservazione è l'AE per quella singola osservazione, ma mediato su tutti i possibili risultati (la somma sul risultato), con la probabilità prevista P(risultato) come peso. La seconda riga esprime che questo coincide con il valore atteso della distanza assoluta tra osservazione e risultato, quando il risultato è distribuito secondo la distribuzione di probabilità.
Che corsa! Non ci siamo ancora, ma quasi: l'AE* non è esattamente il punteggio di probabilità classificato, e non abbiamo ancora idea da dove derivi questo nome ingombrante.
L'AE* sopra definito ha una proprietà indesiderabile: quando la distribuzione vera è una distribuzione di Poisson con un certo valore medio, l'AE* più basso e migliore non si ottiene quando corrisponde a quel valore medio, ma per uno leggermente più piccolo. Se la tua previsione vince in AE*, probabilmente è distorta e sottostima. Il motivo è che l'ampiezza assoluta della distribuzione aumenta con il valore medio, il che favorisce valori medi più piccoli (ancora una volta un'opportunità per pubblicizzare i precedenti post del blog [link a Forecasting Few is Different 1&2]). Questo problema è risolvibile: dobbiamo sottrarre metà dell'ampiezza attesa della distribuzione per tenerne conto, cioè la distanza attesa tra due risultati casuali presi entrambi dalla distribuzione prevista. Infine, questo ci dà il punteggio di probabilità classificato:
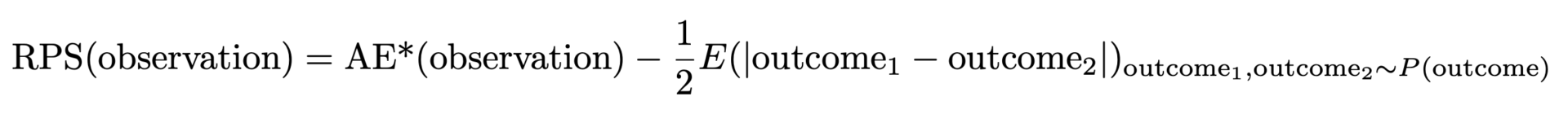
Ma perché questo è chiamato Ranked Probability Score (RPS) e perché è così impopolare? L'RPS è solitamente introdotto tramite formule astratte contenenti molte probabilità, funzioni a gradini, probabilità cumulative. Viene spesso presentato con un'interpretazione puramente teorica della probabilità, che ha molto senso se si è interessati alla teoria della probabilità e alla statistica, ma che rimane inaccessibile ai praticanti. È davvero notevole che le due formulazioni – il nostro "AE migliorato" e quello teorico della probabilità – coincidano: il brutto anatroccolo (agli occhi del praticante) si rivela diventare un bellissimo cigno.
In che modo il punteggio di probabilità classificato risolve le carenze dell'errore assoluto medio
Nella prima parte di questo post ho sostenuto che il MAE ha proprietà scomode: è a grana grossa, discontinuo e inutile per chi si muove lentamente. RPS, il "MAE migliorato", risolve questi problemi? Certamente!
Nel grafico seguente, l'RPS (linea nera) viene confrontato con l'AE (linea blu), sempre per un'osservazione di 9 (linea tratteggiata rossa). Per le previsioni che sono lontane dal risultato 9, RPS e AE si comportano in modo simile e RPS rimane solo leggermente al di sotto di AE. Quando la media prevista e l'osservazione coincidono a 9, AE raggiunge lo zero, mentre RPS è un po' più scettico: poiché RPS è consapevole della distribuzione, giudica che colpire il risultato esattamente con la mediana della distribuzione prevista potrebbe anche essere dovuto al caso: forse il vero tasso di vendita in quel giorno era 7, E siamo stati solo un po' fortunati che la domanda osservata fosse di 9. Pertanto, l'RPS non tocca mai lo 0: nessun risultato individuale dimostra in modo inequivocabile che una previsione probabilistica era corretta. Quando ci si allontana dal risultato 9, l'AE è severo e penalizza immediatamente l'"essere fuori" con il rispettivo costo. L'RPS è più benevolo qui, e non aumenta così rapidamente come fa l'AE, riflettendo che "essere un po' fuori posto" potrebbe essere dovuto alla sfortuna, e non ha bisogno di essere sanzionato immediatamente. Questo si adatta molto meglio alla realtà aziendale: le operazioni sono spesso pianificate in modo da tollerare lievi deviazioni. Tutti vogliono, ma nessuno si aspetta seriamente una previsione deterministica, e ci sono scorte di sicurezza che ne tengono conto. Una volta che le deviazioni sono maggiori, iniziano a indurre costi reali.
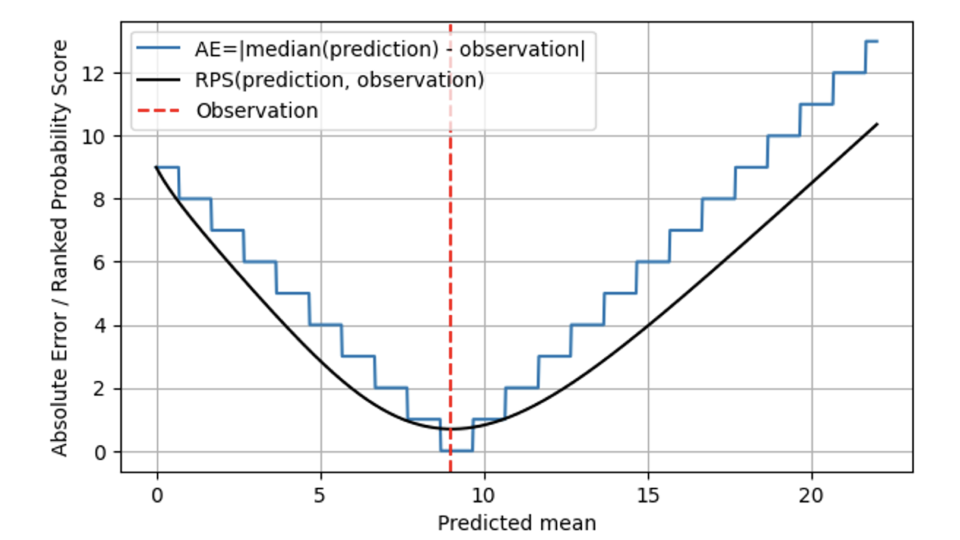
Nel complesso, il Ranked Probability Score non "salta" tra valori diversi, ma è, matematicamente parlando, continuo nella media prevista. Per AE, le previsioni di 8,7, 9,3 e 9,6 sono indistinguibili, per RPS diventano distinguibili: l'RPS minimo viene raggiunto esattamente a una media prevista di 9.
Per gli slow-mover, l'RPS aiuta, ma non è una pillola magica: rimarrà sempre difficile distinguere un prodotto che vende una volta ogni 100 giorni da uno che vende una volta ogni 200 giorni, anche se si utilizza l'RPS. Tuttavia, RPS assume valori diversi anche per piccole stime diverse come 0,6, 0,06 e 0,006.
L'RPS aiuta a risolvere molti dei problemi del MAE, ma c'è una sfida che nemmeno l'RPS risolve: l'inevitabile scalabilità che fa sì che i venditori lenti e veloci si comportino in modo diverso. I metodi che rendono le metriche compatibili con la scalabilità (descritti in alcune parti di questo blog [collegamenti a Forecasting Few is different 1&2]) possono, tuttavia, essere applicati a RPS nello stesso modo in cui sono stati applicati a AE. Rispetto al MAE relativo, l'RPS medio relativo (l'RPS medio diviso per l'osservazione media) ha una forma molto più uniforme in questo grafico che mostra il miglior valore ottenibile per entrambe le metriche:
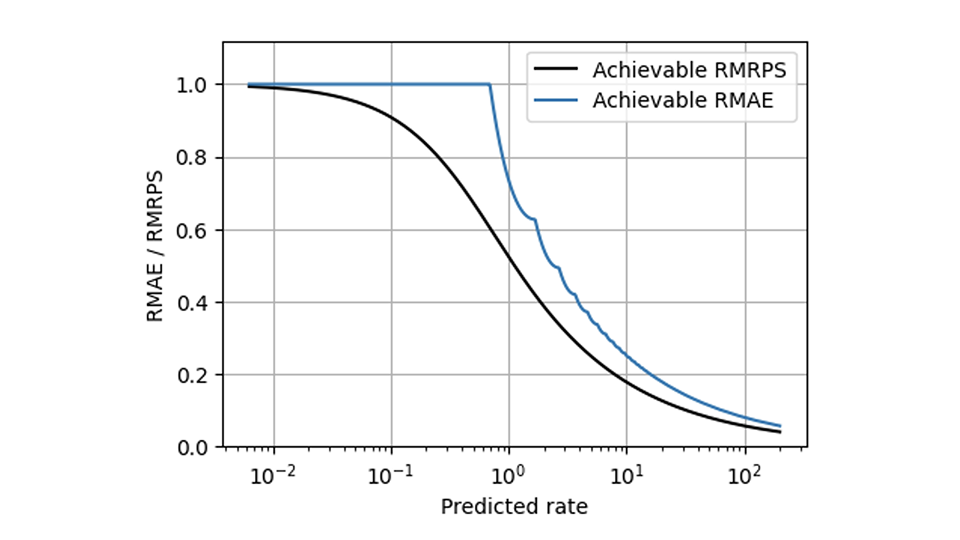
Quando dovresti usare MRPS invece di MAE?
Le previsioni significative non sono mai deterministiche e certe, ma probabilistiche e incerte, di cui bisogna tenere conto nella valutazione. Dire che agli esseri umani non piace l'incertezza è un grande eufemismo: gli esseri umani odiano l'incertezza. Le persone sono disposte a mettere a repentaglio un sacco di utilità attesa per raggiungere la certezza perfetta (che è, quando il rischio è fatale, una cosa ragionevole da fare). Quando agli stakeholder aziendali viene detto che una previsione fornisce "solo" una previsione probabilistica, spesso ne vogliono invece una deterministica, e i previsori devono deluderli rifiutandosi di costruirla. Ma rendere esplicita l'inevitabile incertezza non è un segno di debolezza, ma di affidabilità.
Condensare l'intero potere espressivo di una distribuzione di probabilità, che contiene la probabilità di ogni risultato pensabile, in un singolo numero è semplicistico, grossolano e rozzo come sembra, anche se questo è ciò che si deve fare operativamente quando si fanno scorta di articoli. Da un punto di vista concettuale, il Punteggio di Probabilità Classificato fornisce quindi una risposta molto migliore alla domanda "quanto è lontano il risultato dalla previsione?" rispetto all'Errore Assoluto.
Ogni volta che la natura probabilistica della previsione è irrilevante, la differenza tra AE e RPS diventa trascurabile e AE e RPS possono essere utilizzati in modo intercambiabile (il primo è più semplice da calcolare rispetto al secondo, il secondo assume valori leggermente più piccoli). Cioè, quando l'ampiezza della distribuzione di probabilità è molto più piccola degli errori tipici che si verificano, io, come previsore, non sarò in grado di incolpare gli errori che si verificano a "rumore inevitabile contro il quale non si può fare nulla". Ad esempio, quando prevedo che alcuni articoli verranno venduti 1000 volte, e non sono particolarmente ambizioso e sarei già felice quando i risultati sono da qualche parte tra 800 e 1200, la differenza tra l'utilizzo di RPS e AE diventa marginale. Per semplicità, dovrei quindi attenermi a AE.
Ogni volta che tocchiamo il regime medio-lento, cioè quando prevediamo valori medi come 0,8, 7,2 o 16,8, fa differenza se condensiamo la distribuzione in un singolo numero per valutare l'AE o seguiamo il percorso leggermente più complesso utilizzando RPS. Quando si prevede "1", ciò che intendiamo dire è che la probabilità di osservare "1" è solo del 37% circa, così come la probabilità di osservare 0. Trascurare la natura probabilistica delle previsioni in regime di vendita medio-lenta è quindi pericoloso e fuorviante. Ma ora sapete come tenere conto della distribuzione di probabilità: utilizzando il Punteggio di Probabilità Classificata, che spero ora vediate anche come il bellissimo cigno della fauna selvatica della valutazione previsionale, che riesce a rendere felici sia gli statistici che i professionisti.













