L'errore assoluto medio è la prima scelta per i professionisti quando si tratta di valutare il proprio modello, grazie alla sua semplice definizione e alla sua intuitiva rilevanza aziendale. La metrica di valutazione Ranked Probability Score, al contrario, non è davvero una funzione affascinante a prima vista: il suo nome deterrente si adatta bene alla sua ingombrante definizione formale, che spiega che quasi nessun professionista della supply chain lo conosce, figuriamoci lo usa. Ma si stanno perdendo! Il Ranked Probability Score è la naturale estensione dell'Errore Medio Assoluto nell'ambito delle previsioni probabilistiche, cioè alle previsioni che "conoscono" la propria incertezza. Viene fornito con un'interpretazione intuitiva e risolve molti dei seri problemi dell'errore assoluto medio. Il punteggio di probabilità classificato riflette il business anche meglio dell'errore assoluto medio e tiene conto dell'incertezza statistica, riconciliando così la teoria statistica della torre d'avorio con la pratica quotidiana.
Uno standard aziendale plausibile: l'errore assoluto medio
"Quale metrica utilizzare per valutare il modello di previsione della domanda?"
A questa domanda si risponde tipicamente con "Errore Assoluto Medio" e su basi abbastanza solide. L'errore assoluto (AE) spesso riflette ragionevolmente il costo di una previsione "sbagliata": quando prevedo che verranno venduti 8 cesti di fragole, ne faccio scorta 8, ma la domanda reale è 9, ho un AE di 1 e 1 cliente insoddisfatto si rivolge alla concorrenza. Quando la mia previsione è di 11 cestini per la stessa domanda di 9, l'AE è 2 e ho 2 cesti di fragole da smaltire. Per il risultato osservato 9, l'AE è mostrato dalla linea blu nel grafico seguente in funzione della previsione:
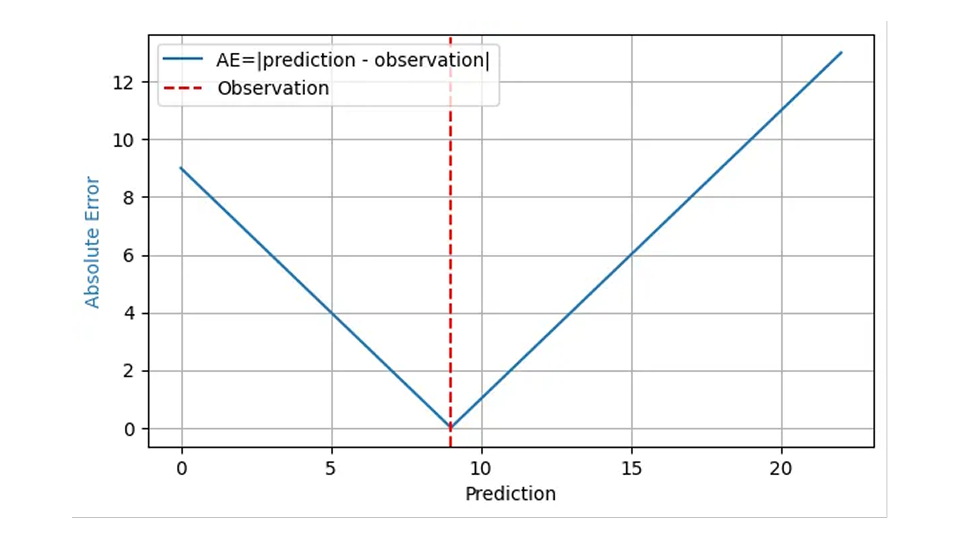
Poiché l'impatto finanziario di un errore di previsione è in genere proporzionale all'errore di previsione stesso, la media dell'AE in molte previsioni e risultati, l'errore assoluto medio (MAE), riflette il costo aziendale, almeno nell'ipotesi che un pezzo di scorte in eccesso abbia lo stesso impatto finanziario di un pezzo di scorte in eccesso. L'errore quadratico medio (MSE) valuterebbe che "essere fuori di uno" diventa più costoso, quanto più grande è già l'errore, cosa abbastanza irrealistica nel mondo degli affari. L'errore percentuale assoluto medio (MAPE), la media dell'evento avverso normalizzato, la media (evento avverso/risultato osservato), soffre di gravi insidie impreviste (come descritto in questo precedente post del blog) e può essere tranquillamente ignorato per la previsione della domanda.
Pertanto, si consiglia ai professionisti di utilizzare il MAE o la sua variante normalizzata MAE relativo, RMAE = MAE / Mean(outcome), come prima semplice scelta per valutare i loro modelli. I valori tipici di MAE e RMAE sono, tuttavia, dipendenti dalla scala: la previsione per le bottiglie di latte (venditori veloci) arriverà naturalmente con un MAE più grande e un RMAE più basso rispetto alla previsione per alcune batterie speciali (vendite lente). Certo, non è facile da capire, motivo per cui il contributo del blog dedicato a questo problema non si adattava nemmeno a un singolo post, ma era diviso in Forecasting few is different part 1 e part 2.
Dato che il MAE è semplice, noto e rilevante, perché scrivere o leggere un post sul blog su un'alternativa? Beh, fidarsi ciecamente di una metrica di valutazione è sicuramente una delle cose più poco scientifiche da fare. Facciamo un'analisi approfondita del MAE per vedere se si comporta davvero come pensiamo che dovrebbe e, in caso contrario, come risolverlo. Per farla breve: incontrerai alcune complicazioni inaspettate e sgradevoli durante la valutazione dell'AE, ma queste vengono risolte delicatamente da una metrica correlata ma piuttosto sottovalutata, il punteggio di probabilità classificato.
Aspetta, non così in fretta! Come valutare l'errore assoluto medio per le previsioni probabilistiche
Finora, abbiamo fatto finta che "una previsione" sia semplicemente un numero, proprio come l'obiettivo previsto stesso (il numero di articoli venduti, che potrebbe essere il numero di cestini di fragole, mele, bottiglie di latte o magliette rosse). Calcolare la differenza tra tale previsione (un numero) e l'osservazione effettiva (un altro numero) non è quindi affatto un problema: prevedo che 10 mele saranno vendute, 7 saranno vendute, l'AE è 3. Non è necessario un dottorato di ricerca in statistica.
Ma c'è una sottigliezza: cosa sarebbe successo se avessi previsto 10,4 mele invece di 10 da vendere? Quale sarebbe stata la mia decisione se il titolo fosse tenuto a portata di mano? Probabilmente avrei comunque ordinato 10 mele, cioè la piccola differenza di 0,4 nella previsione non avrebbe fatto alcuna differenza operativa, il risultato aziendale sarebbe stato lo stesso. Tuttavia, l'errore assoluto sarebbe leggermente maggiore, 3,4 invece di 3. Il comportamento regolare dell'errore assoluto nella previsione nella prima cifra è fuorviante: la differenza tra la previsione e l'effettivo non è la quantità rilevante per l'azienda, ma piuttosto la differenza tra il numero di articoli ordinati e quello effettivo. Perché allora dovrei mai prevedere qualcosa di diverso da un numero intero, quando so che possono verificarsi solo quantità intere?
La ragione di questa discrepanza – prevediamo valori non interi ma misuriamo solo quantità intere – è che la maggior parte delle previsioni non sono "previsioni puntuali" che esprimono una "migliore stima" universale e indipendente dalla valutazione per l'obiettivo, ma forniscono una distribuzione di probabilità (non c'è ancora da preoccuparsi: non è ancora necessario un dottorato di ricerca in statistica). Ci dicono quanto è probabile ogni possibile risultato: quando prevediamo 10,4, non fingiamo che qualche cliente taglierà una mela a pezzi per comprare 0,4 di uno, ma riteniamo che i possibili risultati "11", "12", "13" siano più probabili rispetto a una previsione di 10,0. Le previsioni non sono quindi solo numeri che possono essere confrontati con l'obiettivo, ma funzioni. Anche se la discussione si applica a qualsiasi distribuzione, assumerò in questo post del blog che la distribuzione di probabilità prevista sia la distribuzione di Poisson (dai un'occhiata ai nostri post del blog correlati qui e qui).
Vedi qui quale distribuzione di probabilità affermiamo implicitamente quando prevediamo 1.3, 3.8 o 11.7:
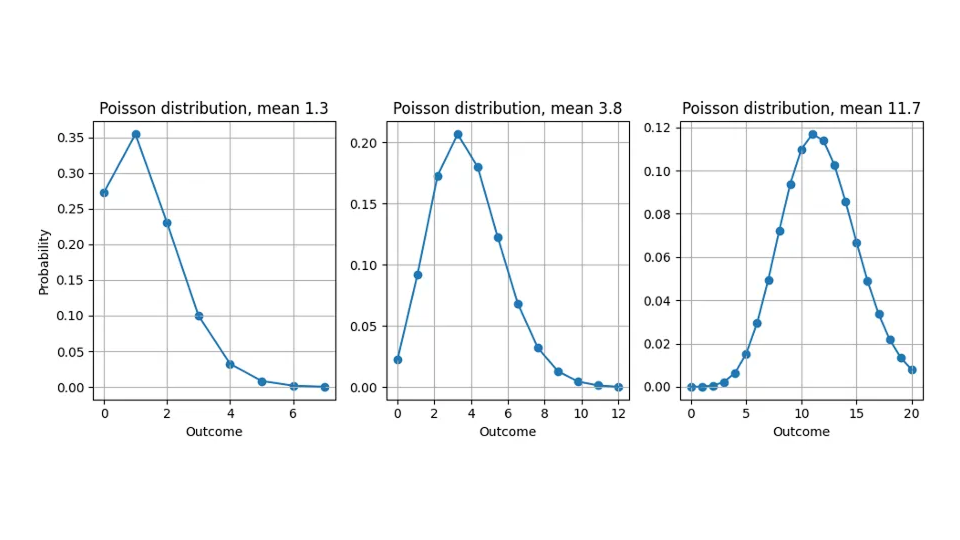
Torniamo alla valutazione dell'errore assoluto: come possiamo sottrarre una funzione da un numero? Sottrarre 7 articoli venduti da una distribuzione di probabilità non ha senso. Abbiamo bisogno di riassumere la distribuzione di probabilità prevista per un singolo numero per rendere possibile un confronto. Questo numero di riepilogo è chiamato stimatore di punti, che può quindi essere sottratto dal valore effettivo osservato per produrre l'errore.
Le distribuzioni di probabilità possono essere riassunte in molti modi: la media è la più immediata, ma le distribuzioni possono anche essere riassunte dal loro risultato più probabile (la loro moda), dal risultato che divide la distribuzione di probabilità in due metà uguali (la loro mediana) o da altre prescrizioni.
In quello zoo di stimatori puntuali, alcuni sembrano più naturali di altri: possiamo semplicemente scegliere il riassunto che ci piace di più? No, lo stimatore di punti corretto è fissato dalla metrica di valutazione scelta. In altre parole: puoi scegliere quale metrica di errore valuta la mia previsione (MAE, MAPE, MSE...), ma poi scelgo come riassumere la previsione per quella valutazione. Il mio stimatore di punti per vincere al MAE sarà diverso da quello per vincere al MSE, per non parlare del MAPE. Questa scelta può sembrare arbitraria, forse anche disonesta per te, ma riflette l'immenso potere espressivo delle previsioni probabilistiche: contengono molte più informazioni di una singola "migliore ipotesi". A seconda di come vengono valutati, di come il "migliore" è effettivamente definito dalla metrica di errore, il valore che vince per un determinato metodo di valutazione viene scelto di conseguenza. In altre parole: la domanda "Dammi la tua migliore previsione" è priva di significato finché non è chiaro come viene definito il "migliore". Una singola previsione probabilistica può produrre molti stimatori di punti diversi, o "migliori ipotesi", a seconda di come viene valutata la previsione.
Per l'errore al quadrato (SE), lo stimatore di punti è la media della distribuzione. Per l'Errore Percentuale Assoluto (APE), lo stimatore di punti è un funzionale davvero contro-intuitivo con cui non vi disturberò, il che porta a paradossi inaspettati nelle valutazioni MAPE.
L'errore assoluto richiede la mediana di distribuzione, non la media, e sì, questo conta
Per AE (Absolute Error), lo stimatore di punti corretto risulta essere la mediana. Sì, la mediana, e non la media, e no, non possiamo semplicemente usare la media. Lasciate che vi spieghi perché solo la mediana può essere ottimale per l'AE. Prendiamo una previsione, cioè una distribuzione, e lasciamo che sia la distribuzione di Poisson con media 3,8 e mediana 4. Quanti articoli fai scorta quando ti viene data questa previsione? Il risultato è necessariamente un numero intero, non può essere 3,8. Per trovare la giusta quantità di stock, scegliamo la stima in modo tale che l'AE che troviamo in media osservando i risultati di quella distribuzione sia il più piccolo possibile.
Cerchiamo il giusto stimatore di punti che condensi l'intera distribuzione in un unico numero, la migliore quantità di stock operativamente. In questa figura, provo tre diverse stime (3, 4, 5):
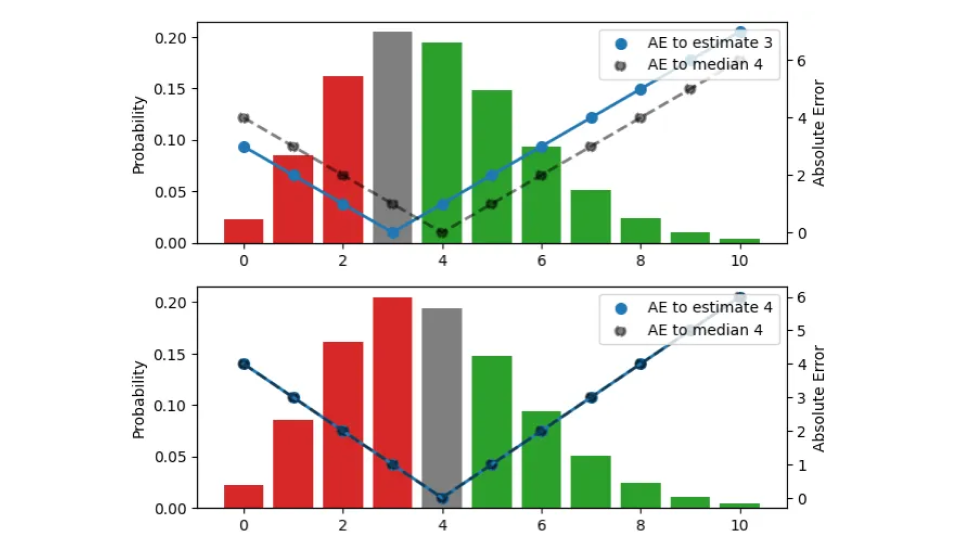

La distribuzione di probabilità, visualizzata dalle barre (scala di sinistra), è la stessa nei tre pannelli. Il pannello superiore visualizza la stima 3, in quello centrale la stima è 4, in quello inferiore è 5. L'AE tra la stima e gli esiti è indicato dai punti blu, collegati dalla linea continua (scala destra), l'AE rispetto alla mediana 4 è indicato da punti neri, collegati da una linea tratteggiata. Ad esempio, quando la stima è 3 (pannello superiore), l'errore per il risultato 3 svanisce e la linea continua blu raggiunge 0. Se l'osservazione è 4 o 2, l'errore è 1.
Il colore delle barre indica se un risultato previsto contribuisce all'errore assoluto perché è più piccolo (rosso) o più grande (verde) della stima, l'altezza della barra è la probabilità che si verifichi. Quando un risultato corrisponde alla stima, contribuisce zero all'errore e viene visualizzato in grigio. Spostando la stima verso l'alto di un'unità, ci spostiamo verso il basso di un pannello e tutte le osservazioni sotto le barre rosse e sotto la barra grigia contribuiscono a un'unità di errore in più per la nuova stima spostata: per la stima precedente 3, il risultato 2 aveva errore 1, ma per la stima 4, lo stesso risultato ha errore 2. D'altra parte, tutte le osservazioni che avevano barre verdi ora contribuiscono a un'unità di errore in meno dopo lo spostamento: per la stima 3, il risultato 5 aveva errore 2, per la stima 4, l'errore diminuisce a 1.
Riassumiamo cosa succede quando la stima viene aumentata di un'unità: il valore atteso di AE sotto la distribuzione aumenta per quei risultati che sono inferiori o uguali alla stima (li abbiamo sovrastimati anche più di quanto abbiamo fatto) e diminuisce per quelli che sono più grandi della stima (li abbiamo sottostimati meno). L'aumento è proporzionale all'area totale delle barre rosse e grigie, la diminuzione è proporzionale all'area delle barre verdi.
In piena analogia, quando si riduce la stima di un'unità, le osservazioni sotto le barre verdi o sotto la barra grigia contribuiscono a un'unità di errore in più ciascuna, e tutte le osservazioni nelle barre rosse contribuiscono a un'unità di errore in meno.
Per una data distribuzione, spostando la stima verso l'alto e verso il basso di uno aumenta o diminuisce l'errore assoluto atteso risultante, e possiamo cercare la stima puntuale corretta cercando il minimo. Potresti aver già ideato questa regola empirica: se, per la stima attuale, la maggior parte dei risultati sono sottostimazioni, diminuisci la stima; Se la maggior parte dei risultati sono previsioni eccessive, aumentalo. Solo quando la differenza tra le masse di probabilità relative alle sovra e sottostimate (la differenza tra le aree totali delle barre "rosse" e "verdi") è inferiore alla barra grigia, non si può migliorare ulteriormente l'errore. Questo è il caso del pannello centrale: la stima è tale che le masse di probabilità al di sotto e al di sopra di essa quasi coincidono, in modo tale che muoversi in entrambe le direzioni aumenterebbe l'errore totale. Questa stima corrisponde alla mediana: quando ti viene data una distribuzione di probabilità, lo stimatore di punti che minimizza l'errore assoluto sarà superiore o inferiore ai risultati nella metà dei casi.
Credo che valga la pena sottolineare questo punto, perché spesso non viene preso in considerazione: quando 7,3 è la migliore stima per la media di una distribuzione, il modo corretto di valutare l'errore assoluto rispetto a un'osservazione, diciamo, di 9, non è quello di sottrarre 7,3 da 9, ma di sottrarre la mediana di quella distribuzione (che è 7 per la distribuzione di Poisson), dal 9. Operativamente, 7 è esattamente il numero di articoli che faresti scorta, data una previsione di 7,3. Sorprendentemente, non ti aiuta avere una stima precisa del valore medio per le decisioni sulle azioni, non importa se la previsione è 7,1 o 7,3: Devi decidere per un numero intero. Tuttavia, quando si aggregano le previsioni a un livello superiore per la pianificazione, la distinzione tra 7,1 e 7,3 diventa importante.
Questa distinzione tra media e mediana può sembrare come spaccare il capello in due: dopo tutto, il valore che divide la probabilità in due metà uguali e la media di quella distribuzione sembrano molto simili, e sono vicini per la maggior parte delle distribuzioni benevole (come la distribuzione di Poisson che è pertinente per la vendita al dettaglio). Tuttavia, due distribuzioni possono avere la stessa media, ma mediane diverse; Altre due distribuzioni potrebbero coincidere nella mediana ma differire nella loro media. L'uso della media e della mediana come sinonimi ti impedirebbe di trovare davvero la previsione migliore.
Le carenze inaspettate dell'Errore Assoluto Medio
Ora sappiamo come valutare l'errore assoluto per le previsioni probabilistiche: riassumiamo la distribuzione per la mediana dello stimatore puntuale (il numero di elementi che accumuleremo), sottraiamo quella mediana dal risultato osservato e prendiamo il valore assoluto. Ho cercato di visualizzare questo nel seguente grafico:
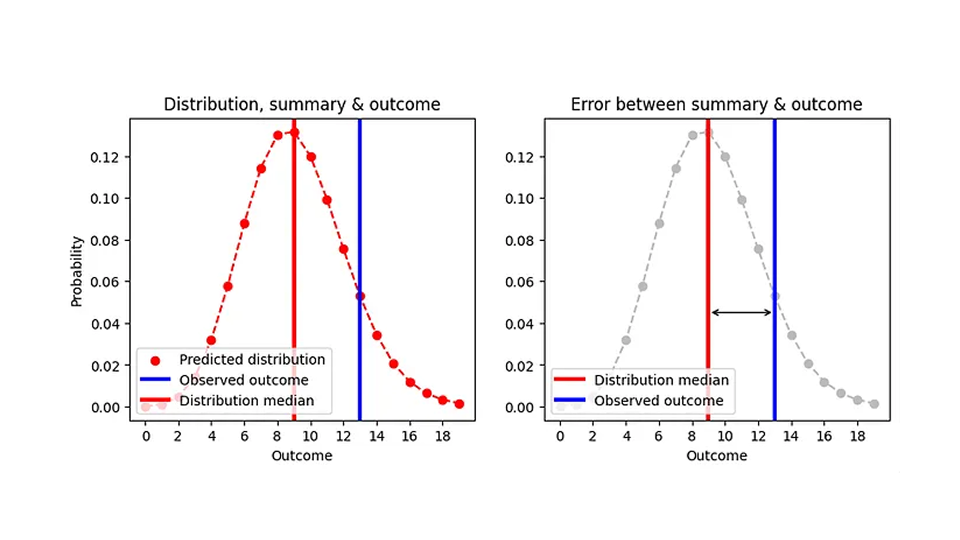
Poiché la mediana è sempre un numero intero, due distribuzioni molto diverse possono produrre lo stesso errore assoluto. Ad esempio, l'AE per una previsione di Poisson di 8,7 (mediana=9) e per una previsione di Poisson di 9,6 (mediana=9) sono le stesse, anche se le previsioni sono chiaramente diverse, come vediamo in questa figura:
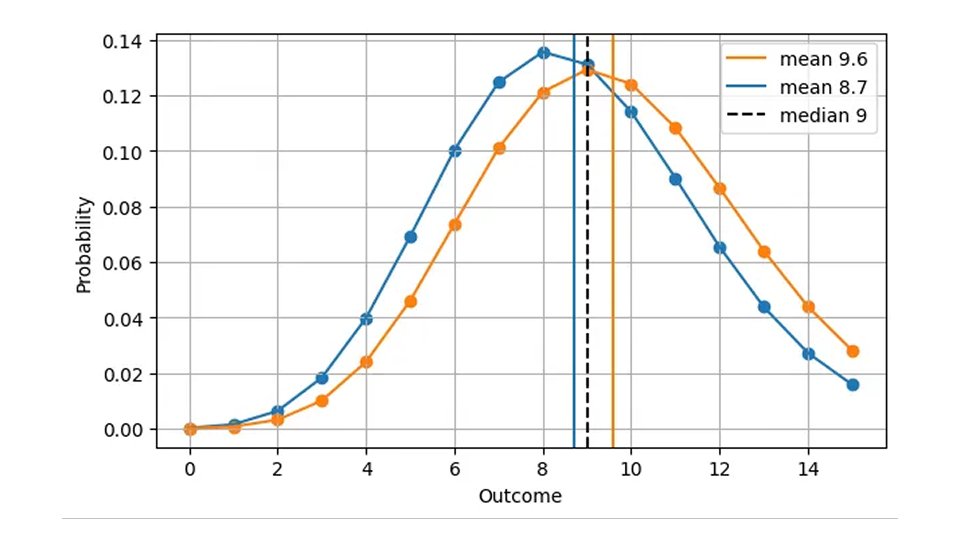
Questo ha senso dal punto di vista operativo: in entrambi i casi, la cosa giusta da fare è avere 9 articoli in magazzino in un determinato giorno. Di conseguenza, una versione più realistica della prima figura, AE in funzione della previsione, è la seguente.
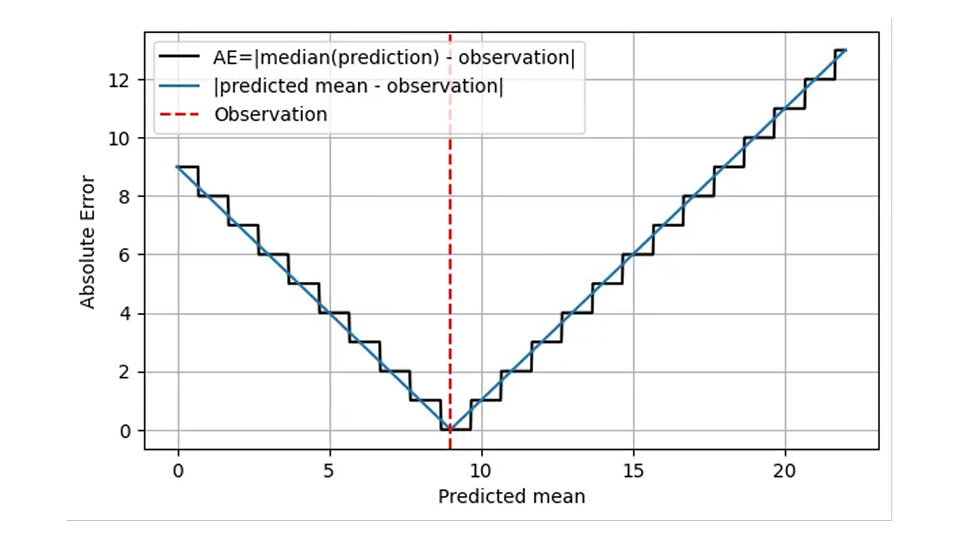
L'AE viene calcolato utilizzando la mediana della previsione (linea nera) e assume solo valori interi. Sto diventando un po' più specifico su cosa significhi l'asse x: non è solo la "previsione", ma la media prevista.
Questa forma della scala implica che AE è a grana grossa e imprecisa: possiamo, a occhio, distinguere le distribuzioni con media 8,7 e 9,6, ma AE non può! Il MAE da solo non ti aiuterà a migliorare la precisione di una previsione oltre una certa soglia, il che è piuttosto drammatico per gli elementi che si muovono lentamente: la differenza relativa tra 1,7 e 2,6 ammonta al 53%, mentre l'AE di una previsione di 1,7 e quello di una previsione di 2,6 sono gli stessi! Questo comportamento a grana grossa sta arrivando con brutti salti, discontinuità ai valori ai quali la mediana della distribuzione salta da un valore intero all'altro. Dal punto di vista operativo, non c'è differenza nel prevedere 1,7 o 2,6 per un determinato giorno, luogo e articolo: la quantità giusta da scorta è 2. Le previsioni vengono tuttavia utilizzate anche su livelli di aggregazione più elevati per la pianificazione. A un livello così alto, si nota effettivamente la differenza tra 1,7 e 2,6: per i prossimi 100 giorni, fa un'enorme differenza se si ordinano 170 o 260 articoli dal fornitore.
Quando la media prevista è inferiore a circa 0,69 per periodo di tempo di previsione (una vendita lenta), la previsione che ti dà il miglior errore assoluto è 0. Abbastanza drammaticamente, abbiamo lo stesso Errore Assoluto per una previsione di 0,6, 0,06 e 0,006, anche se abbiamo attraversato due ordini di grandezza! La previsione 0 è del tutto inutile nella supply chain, poiché si entra nel circolo vizioso delle previsioni 0 perfette: si accumula 0, si vende 0 e lo 0 previsto in precedenza si è autoavverato.













