Nelle previsioni al dettaglio, la quantità di interesse è la domanda dei clienti per un determinato prodotto, ad esempio quanti cesti di fragole vengono richiesti. In pratica, si osserva una quantità leggermente ma significativamente diversa, ovvero le vendite registrate. Le vendite riflettono la domanda, ma sono limitate dalla capacità, cioè dal livello delle scorte: quando 20 panieri sono richiesti, ma 12 sono disponibili, solo 12 vengono venduti e gli 8 clienti che erano disposti ad acquistare non sono stati soddisfatti. La distinzione tra vendite e domanda può sembrare come spaccare il capello in quattro, ma questo post del blog ti mostrerà perché confondere le vendite con la domanda porta a corsi di formazione distorti e valutazioni errate dei modelli. Imparerai in che modo le scorte limitate influiscono sulle vendite e come aggirare le insidie più importanti per affrontare con sicurezza le situazioni del mondo reale che coinvolgono le scorte limitate.
Domanda e vendite
Qual è la previsione più precisa a cui puoi pensare, una previsione della domanda sempre corretta su cui puoi piazzare qualsiasi scommessa? In molte situazioni, la risposta è: basta prevedere "0" tutto il tempo! In vista di una previsione della domanda pari a zero, non verrà ordinato un singolo articolo, nessun articolo sarà sullo scaffale, nessun articolo sarà venduto. La previsione dello zero risulta essere esattamente sul posto, corrispondendo perfettamente alle vendite zero osservate. Questa previsione assolutamente accurata non è, ovviamente, la previsione che renderà felice il tuo manager.
Questo esempio estremo illustra che bisogna stare attenti a cosa chiedere: l'obiettivo di un rivenditore non è quello di produrre una previsione precisa, ma di gestire un'attività sostenibile. Il paradosso mette anche in luce un dilemma fondamentale nella previsione della domanda: la previsione stessa influenza il livello di stock che viene eventualmente fornito, compromettendone la valutazione. Si potrebbe obiettare che questa influenza esiste per buone ragioni, è per questo che è stata fatta la previsione! Ma il livello delle scorte stabilisce un limite superiore al numero di articoli che possono essere venduti, il che limita artificialmente i valori di vendita che possono essere osservati. Ciò porta a una discrepanza tra la domanda ipotetica ("quanto viene chiesto") e le vendite osservate ("quanto è stato venduto"). Le vendite osservate sono la domanda reale o le scorte disponibili, a seconda di ciò che è inferiore.
In questo post del blog, vi convincerò che non c'è modo di evitare un rigoroso trattamento probabilistico del problema della domanda rispetto alle vendite. La distinzione tra domanda e vendite, il trattamento meticoloso di queste quantità e di ciò che prevediamo e osserviamo esattamente è la chiave per il successo e la corretta formazione e valutazione del modello.
Per rendere le cose tangibili (e saporite), prendiamo in considerazione un rivenditore che vende cesti di fragole fresche. Il numero di panieri venduti con valori interi può quindi essere trattato come "pezzi". Sfortunatamente, questi prodotti alimentari ultra-freschi vanno sprecati quando non vengono venduti durante il giorno. Pertanto, l'eccesso di ordini, cioè l'avere in magazzino più di quanto richiesto, è costoso e dovrebbe essere evitato. D'altra parte, immagina di essere pronto per le fragole, ma sono già esaurite quando le cerchi nel tuo supermercato locale: diventi un cliente frustrato, la cui disponibilità a pagare non è stata raccolta. Quindi, anche gli ordini insufficienti, avendo meno scorte di quanto richiesto, sono costosi, sia in termini di soddisfazione del cliente che di mancati ricavi e profitti.
Un rivenditore dovrebbe ordinare il giusto numero di cesti di fragole per bilanciare attentamente gli sprechi e le vendite perse. Naturalmente, per risolvere questo problema di ordinazione, è necessaria una precisa previsione della domanda che preveda veramente quanti cestini vengono richiesti e non quanti ne vengono venduti (ricordate la profezia dello "0" che si autoavvera sopra).
Quanto venderemo?
Immergiamoci un po' più a fondo nelle previsioni della domanda e analizziamo il loro significato. Una previsione della domanda ci dice quanti articoli verranno richiesti. Ma cosa significa esattamente quando "verranno richiesti 9,7 cestini"? Chiaramente, non si può vendere un numero frazionario di cesti di fragole, l'interpretazione letterale è ridicola. Tuttavia, accettiamo e comprendiamo intuitivamente la previsione, e la interpretiamo come un'affermazione sul numero medio atteso di panieri venduti, il numero di panieri che vendiamo in media quando la stessa situazione si è ripetuta molte volte (e le scorte sono sempre sufficienti, cosa che per ora assumeremo). Pertanto, la nostra previsione nasconde implicitamente una certa distribuzione di probabilità, cioè una certa concezione di quanto sia probabile vendere 1, 2, 3, ... panieri, poiché indica solo le vendite medie previste. Quali siano queste probabilità, o quanto le singole osservazioni (cioè i numeri di vendita effettivi) si trovino intorno a quella media di 9,7, è tralasciato.
Solleviamo il tappeto sotto il quale è stata nascosta la distribuzione di probabilità per vedere come dovrebbe apparire. Utilizzeremo il grafico seguente per illustrare il nostro esempio. A priori, le distribuzioni di probabilità con un valore atteso di 9,7 possono assumere forme molto diverse: si pensi a una probabilità del 51,5% di incontrare zero e a una probabilità del 48,5% di trovare 20, mostrate nel pannello di sinistra. Ciò si traduce in una media di 9,7, anche se non si osserva mai nulla di vicino a 9,7, come 9 o 10, ma solo valori estremi come 0 o 20. La distribuzione di probabilità del pannello centrale assegna una probabilità del 70% a 10 e una probabilità del 30% a 9; Ha anche il valore atteso 9,7, ma la massa di probabilità è molto più concentrata tra valori vicini alla media, il che diventa quindi una buona stima per il numero tipico di vendite. L'insieme delle distribuzioni con una media di 9,7 è infinitamente grande, e la maggior parte di queste distribuzioni si comporterà male (o "patologica" come piace dire ai matematici). Fortunatamente, possiamo assumere distribuzioni di probabilità semplici e ben comportate, come la distribuzione di Poisson nel pannello di destra (leggi il post del blog Forecasting few is different per sapere perché è una scelta ragionevole).
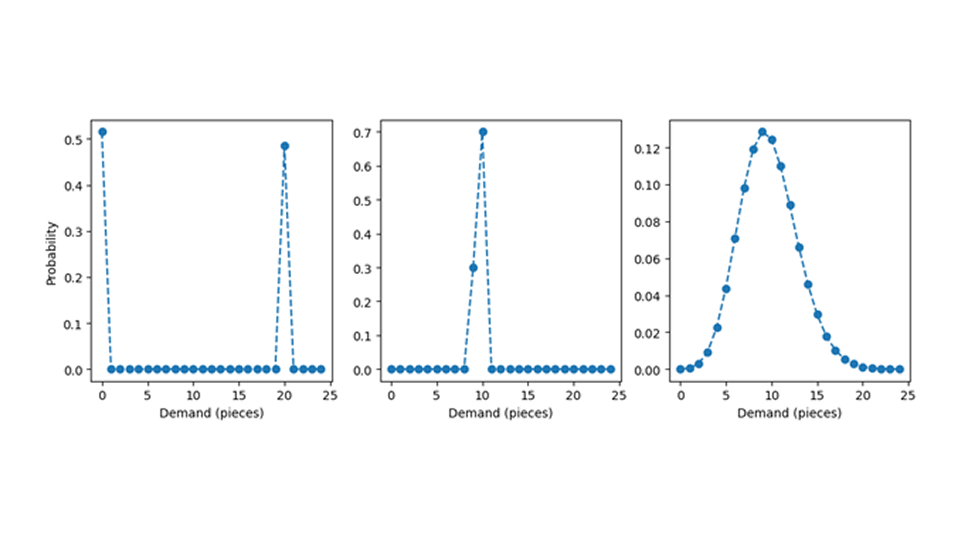
In tutto questo testo, assumiamo che la previsione produca la media di una distribuzione di Poisson prevista, e che la domanda sia veramente distribuita a Poisson, cioè che la previsione sia corretta. Anche questo scenario idealizzato ospiterà abbastanza complessità da giustificare un post sul blog.
In che modo le azioni limitate censurano le informazioni
Diamo ora il benvenuto alla capacità finita nel gioco. Data una distribuzione della domanda, otteniamo la distribuzione delle vendite mappando ogni possibile valore della domanda al valore di vendita risultante. Per tutti i valori della domanda che sono inferiori o uguali al numero di scorte disponibili, la domanda si traduce semplicemente 1:1 in vendite: quando ci sono 12 panieri disponibili, 5 panieri richiesti danno come risultato 5 venduti, 12 panieri richiesti portano a 12 venduti. Quando la domanda è maggiore delle scorte, in altre parole, quando la capacità non è sufficiente, le vendite sono limitate da quel valore di scorte: quando vengono richiesti 13, 25 o 463 panieri, ne verranno venduti solo 12. Quando tutte le azioni vengono vendute, lo chiamiamo un evento di "capacity hit". La massa di probabilità associata alla domanda di 13, 25 o 463 panieri, tuttavia, deve "andare da qualche parte" e si aggiunge efficacemente alla probabilità che vengano richieste le scorte totali. Le distribuzioni della probabilità di vendita per una domanda media di 9,7 e diverse capacità (16, 12, 8) sono mostrate nella figura seguente.
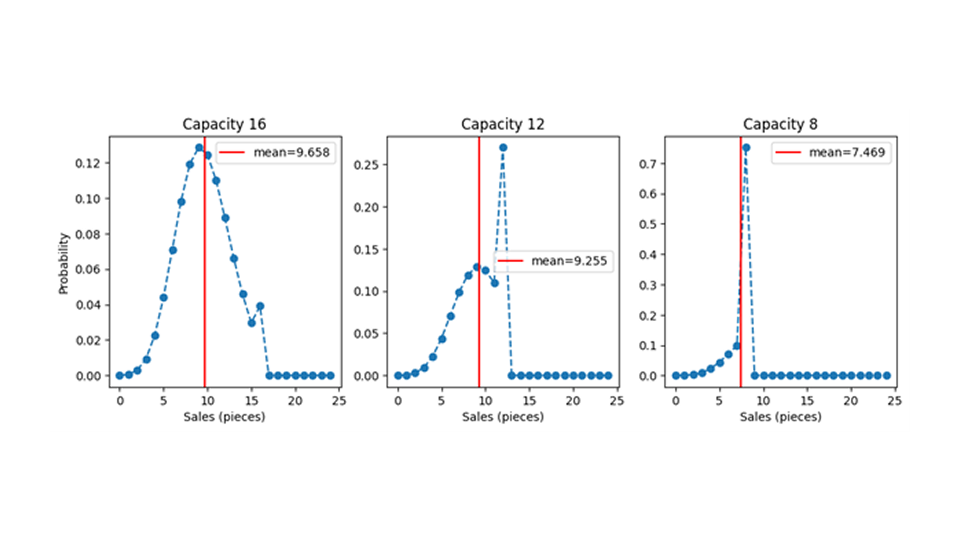
La capacità finita sta censurando la domanda in modo da rimuovere l'informazione: quando si mette su una capacità di 16 e si osserva un colpo di capacità, cioè 16 vendite, si può solo dedurre che la domanda era almeno 16 – non se era 16, 25 o 7.624. La domanda effettiva ha un valore a te sconosciuto – diciamo, 47 – ma osservi solo 16. A causa della capacità limitata, stiamo davvero perdendo informazioni in modo irrevocabile (e non solo la soddisfazione del cliente). Questa perdita di informazioni rende più difficile addestrare modelli a capacità finita e valutarli.
I grafici mostrano anche le vendite medie attese come linee rosse verticali. Forse sorprendentemente, la capacità finita ha un impatto sul valore atteso delle vendite anche quando la capacità è ancora maggiore della domanda prevista. Cioè, quando prevedi una domanda di 9,7 e fornisci 12 articoli in magazzino, vendi meno di 9,7, in media! In media, devi fare scorta più del previsto per vendere tanto quanto previsto! Questo potrebbe creare confusione: per un singolo evento, le vendite sono solo il minimo della domanda e delle scorte. Ma la media della distribuzione di probabilità di vendita non è necessariamente il minimo della domanda attesa e della capacità, poiché la forma della distribuzione di probabilità deve essere presa in considerazione. La ragione di questo comportamento probabilmente sorprendente è che il valore della domanda media prevista si basa su fluttuazioni intorno alla media che si annullano in media. Cioè, le fluttuazioni negative (a volte, vengono venduti meno di 9,7 articoli) sono bilanciate da quelle positive (a volte, vengono venduti più di 9,7 articoli). Quando la capacità è finita, quelle fluttuazioni positive necessarie vengono soppresse e l'annullamento delle fluttuazioni positive e negative non si verifica più. Ciò spinge le vendite medie attese a valori più bassi, anche quando la capacità è maggiore della domanda media prevista.
Il grafico seguente mostra le vendite attese in funzione della capacità, sempre per una domanda prevista di 9,7. Quando la capacità è molto più grande della domanda prevista (ad esempio, circa 20), gli eventi che sono influenzati dalla capacità finita sono rari. Di conseguenza, il numero di vendite previsto rimane inalterato e vicino a 9,7. Quando la capacità è piccola, diciamo 5, allora è quasi inevitabile che la capacità venga colpita e, in media, venga venduto un valore vicino a quella capacità. Tra le 7 e le 14 circa, avviene una transizione, la capacità ha un impatto forte, ma non totalmente determinante, sulle vendite.
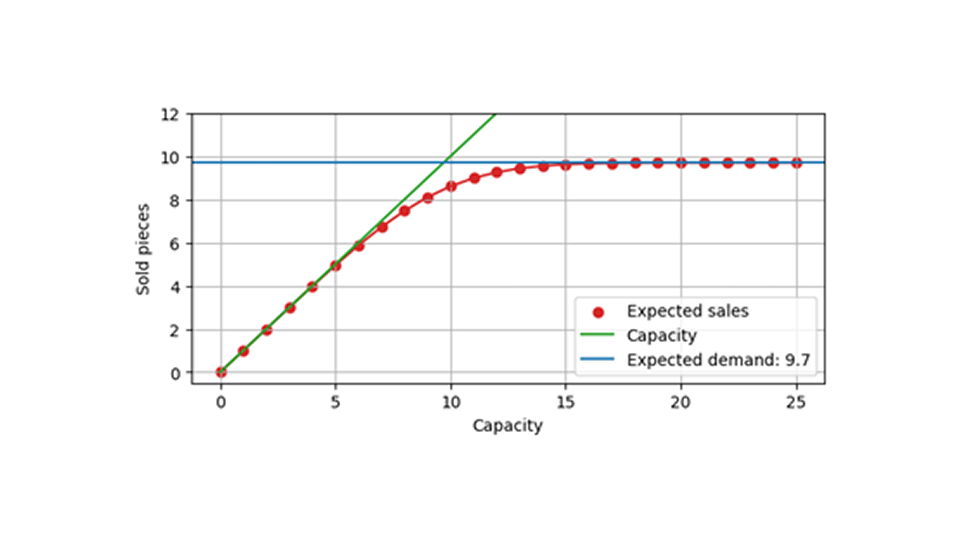
Addestramento e valutazione dei modelli su richiesta censurata
Ora che abbiamo sotto controllo il nostro cavallo di battaglia, ovvero la distribuzione della domanda censurata dalla capacità, capiamo a cosa dobbiamo prestare attenzione quando addestriamo e valutiamo i modelli in tali circostanze.
Dobbiamo distinguere i diversi regimi. Se la capacità fosse colpita ogni giorno, non si saprebbe mai la vera domanda, ma si apprenderebbe solo un limite inferiore ad essa ("abbiamo venduto 5 pezzi, quindi la domanda è stata almeno 5"). Questo è, fortunatamente, uno scenario irrealistico: quando la capacità viene colpita ogni giorno, abbiamo a che fare con molti clienti insoddisfatti e molta domanda insoddisfatta – nessun rivenditore sosterrà a lungo tale modalità operativa. Se sono costretti a farlo da restrizioni dell'offerta, potrebbero prendere in considerazione l'idea di indirizzare la domanda aumentando i prezzi.
All'altro estremo, quando la capacità non viene mai raggiunta, ci godiamo il dolce regime di fare scienza dei dati: leggiamo la vera domanda ogni giorno, possiamo essenzialmente trascurare tutte le discussioni sulla capacità. Ma il sogno del data scientist è l'incubo del responsabile della sostenibilità: un'enorme quantità di rifiuti sarebbe la conseguenza di tale strategia di ordinazione. Data una domanda prevista di 9,7, avremmo bisogno di mantenere 21 articoli in magazzino per esaurire le scorte solo una volta ogni 1.000 giorni.
Pertanto, in genere ci si imbatte in una situazione in cui la domanda a volte raggiunge la capacità (e il prodotto è esaurito in un determinato momento durante una giornata), e a volte no (e alcune scorte rimangono la sera). Ciò è ragionevole, dal momento che è auspicabile un compromesso tra gli obiettivi concorrenti di evitare gli sprechi e di evitare l'esaurimento delle scorte.
Dobbiamo riconoscere che la costruzione del miglior modello possibile è in conflitto con la gestione del miglior business possibile: in una strategia aziendale sostenibile (quando i rifiuti non sono completamente "gratuiti", ma vengono evitati almeno in una certa misura), è inevitabile che i prodotti vadano a volte esauriti. La migliore scienza dei dati, tuttavia, viene eseguita quando è garantito che non si verifichino mai esaurimenti di stock e ogni valore di vendita riflette direttamente la domanda. Dal momento che stiamo facendo scienza dei dati in un contesto aziendale, dovremo convivere con lo scenario intermedio e occasionali rotture di stock.













