Il bias di selezione a posteriori si verifica quando le previsioni probabilistiche e i valori effettivi osservati non vengono raggruppati correttamente quando si valuta l'accuratezza delle previsioni attraverso le frequenze di vendita. Da un lato, il bias di selezione del senno di poi è una trappola insidiosa che ti spinge verso conclusioni sbagliate sul bias di una data previsione probabilistica – nel peggiore dei casi, permettendoti di scegliere un modello peggiore rispetto a uno migliore. D'altra parte, la sua risoluzione e spiegazione toccano fondamenti statistici come la rappresentatività campionaria, la previsione probabilistica, le probabilità condizionali, la regressione alla media e la regola di Bayes. Inoltre, ci fa riflettere su ciò che ci aspettiamo intuitivamente da una previsione e sul perché ciò non sia sempre ragionevole.
Le previsioni possono riguardare categorie discrete : ci sarà un temporale domani? — o quantità continue — quale sarà la temperatura massima domani? Ci concentriamo qui su un caso ibrido: quantità discrete, che potrebbero essere, ad esempio, il numero di magliette vendute in un determinato giorno. Tale numero di vendita è discreto, potrebbe essere 0, 1, 2, 13 o 56; ma certamente non -8,5 o 3,4. La nostra previsione è probabilistica, non pretendere di sapere esattamente quante magliette verranno vendute. Un approccio realistico, ma ambiziosamente ristretto (es. precisa) distribuzione di probabilità è la distribuzione di Poisson. Supponiamo quindi che la nostra previsione produca il tasso di Poisson che riteniamo guidi il processo di vendita effettivo.
Una previsione piuttosto mediocre?
Si supponga che la previsione sia stata emessa, che siano state raccolte le vendite effettive e che la previsione venga valutata tramite tale tabella:
| Frequenza di vendita osservata | Vendite medie osservate | Previsione media |
| Lento 0, 1, 2, pezzi/giorno | 0.804 | 1.373 |
| Medio 3-10 pezzi/giorno | 5.119 | 4.601 |
| Veloce >10 pezzi/giorno | 13.880 | 11.041 |
I dati sono raggruppati in base alla frequenza di vendita osservata: suddividiamo tutti i giorni in gruppi in cui la maglietta è stata venduta poche (0, 1 o 2), intermedie (da 3 a 10) o molte (più di 10) volte. A prima vista, questa tabella grida inequivocabilmente "i venditori lenti sono sovrastimati, i venditori veloci sono sottostimati". La previsione è così palesemente profondamente errata che ci precipiteremmo immediatamente a correggerla, o no?
In realtà, e forse sorprendentemente, va tutto bene. Sì, i venditori lenti sono effettivamente sovrastimati e i venditori veloci sono sottostimati, ma la previsione si comporta proprio come dovrebbe. È la nostra aspettativa – che le colonne "medie delle vendite osservate" e "media delle previsioni" dovrebbero essere le stesse – che è errata. Abbiamo a che fare con un problema psicologico, con le nostre aspettative irrealistiche, e non con una cattiva previsione! Una previsione probabilistica non ha mai promesso né mai manterrà che, per ogni possibile gruppo di risultati, la previsione media corrisponda al risultato medio.
Esploriamo perché è così, come risolvere questo enigma in modo soddisfacente e come evitare pregiudizi simili.
Cosa chiediamo in realtà?
Facciamo un passo indietro ed esprimiamo a parole ciò che la tabella rivela. I dati vengono raggruppati utilizzando le vendite effettivamente osservate, ovvero filtriamo o condizioniamo le previsioni e le osservazioni sulle osservazioni che si trovano in un certo intervallo (vendite lente, medie o veloci). La prima riga contiene tutti i giorni in cui la maglietta è stata venduta 0, 1 o 2 volte, la sua colonna centrale ci fornisce:

cioè la media delle osservazioni nel secchio in cui abbiamo raggruppato tutte le osservazioni che sono 2, 1 o 0 - sicuramente un numero compreso tra 0 e 2, che sembra essere 0,804. La colonna di destra contiene la previsione della media attesa per lo stesso gruppo di osservazioni,

cioè per tutte le osservazioni che sono 2 o meno, prendiamo la previsione corrispondente e calcoliamo la media su tutte queste previsioni.
A priori, non c'è motivo per cui la prima e la seconda espressione debbano assumere lo stesso valore, ma intuitivamente vorremmo che lo facessero: aspettarsi che la previsione della media equipari l'osservazione media non sembra chiedere troppo, non è vero?
| Frequenza di vendita osservata | Vendite medie osservate | Previsione media |
| Lento 0, 1, 2, pezzi/giorno | E (osservazione | osservazione ≤ 2) | E (previsione | osservazione ≤ 2) |
| Medio 3-10 pezzi/giorno | E (osservazione | osservazione ≤ 3, ≤ 10 ) | E (previsione | osservazione ≤ 3, ≤ 10] ) |
| Veloce >10 pezzi/giorno | E (osservazione | osservazione ≥ 11) | E (previsione | osservazione ≥ 11]) |
Previsioni lungimiranti, senno di poi
Coerentemente con la loro etimologia, le previsioni sono lungimiranti e ci forniscono le probabilità per osservare i risultati futuri,
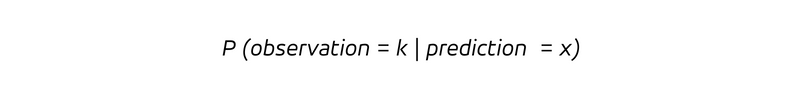
che è la probabilità condizionata di osservare un risultato k, dato che il tasso previsto è x. Poiché abbiamo una probabilità condizionata , consideriamo la distribuzione di probabilità per le osservazioni assumendo che la previsione assuma il valore x. Per una previsione imparziale, il valore atteso dell'osservazione condizionata da una previsione x, cioè l'osservazione media sotto l'ipotesi di una previsione del valore x, è:
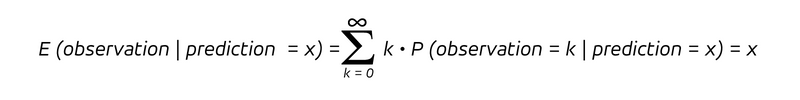
Questo è ciò che promette qualsiasi previsione imparziale: raggruppando tutte le previsioni dello stesso valore x, la media delle osservazioni risultanti dovrebbe avvicinarsi a questo stesso valore x. Sebbene la distribuzione possa assumere molte forme diverse, questa proprietà è essenziale.
Diamo un'occhiata alla tabella: quello che facciamo nella colonna di sinistra non è raggruppare/condizionare per previsione, ma per risultato. La colonna di destra chiede quindi al retrospettivo "qual è stata la nostra previsione media, dato un certo risultato k" invece del prospettico "quale sarà il risultato medio, data la nostra previsione x".
Per esprimere l'affermazione retrospettiva in termini di lungimirante, applichiamo la regola di Bayes,

Le domande retrospettive e quelle lungimiranti sono diverse, così come le loro risposte: compaiono altri termini, P (previsione = x) e P (osservazione = k), le probabilità incondizionate per una previsione e un risultato. Di conseguenza, il valore atteso della previsione media, dato un certo risultato, diventa:

Esempio minimalista
Quale valore assume E (previsione | osservazione = m)? Perché non dovrebbe semplicemente semplificare l'osservazione m?
Nella stragrande maggioranza dei casi, vale E (previsione | osservazione = m) ≠ m. Vediamo perché!
Prendi in considerazione una maglietta che vende altrettanto bene ogni giorno, dopo una distribuzione di Poisson con il punteggio 5. La stessa tariffa prevista, 5, si applica a tutti i giorni. Il risultato, tuttavia, varia. Chiaramente, 5 è una sovrastima per gli esiti 4 e inferiori e una sottostima per gli esiti 6 e superiori. Se raggruppiamo di nuovo in base ai risultati, incontriamo:
| Frequenza di vendita osservata | Vendite medie osservate | Previsione media |
| Lento <5 pezzi/giorno | 3.0082 | 5 |
| Medio 5 pezzi/giorno | 5 | 5 |
| Veloce >5 pezzi/giorno | 7.2844 | 5 |
Ancora una volta, da questa tabella concludiamo che i giorni di vendita lenta sono stati sovra-previsti e i giorni di vendita veloce sono stati sotto-previsti, e lo sono stati effettivamente. Vale per ogni osservazione E (previsione | osservazione = m) = 5, poiché la previsione è sempre 5.
La previsione è ancora "perfetta": i risultati si comportano esattamente come previsto, seguono la distribuzione di Poisson con tasso 5. L'impressione di una previsione insufficiente o superiore è puramente il risultato della selezione dei dati: selezionando i risultati superiori a 5, manteniamo quei risultati che sono superiori alla previsione 5 e sono stati sottostimati; Selezionando i risultati inferiori a 5, manteniamo gli eventi al di sotto della previsione 5, che sono stati sovrastimati. Per una previsione probabilistica, è inevitabile che alcuni risultati siano stati sottostimati e altri siano stati sovrastimati. Aspettandoci che la previsione sia imparziale, ci aspettiamo che la sottoprevisione e la sovraprevisione siano bilanciate per una data previsione m. Quello che non possiamo aspettarci è che quando selezioniamo attivamente le osservazioni sovra-previste o sotto-previste, queste non siano rispettivamente sovra o sotto-previste!
In una situazione realistica, non avremo a che fare con una previsione che assume lo stesso valore per ogni giorno, ma la previsione stessa varierà. Tuttavia, selezionare risultati "piuttosto grandi" o "piuttosto piccoli" equivale a mantenere gli eventi sottostimati o sovrastimati nei bucket. Pertanto, abbiamo E (previsione | osservazione = m) ≠ m in generale. Più precisamente, ogni volta che m è così grande che selezionarlo equivale a selezionare eventi sottostimati, avremo E (previsione | osservazione = m) < m; quando m è sufficientemente piccolo che selezionarlo equivale a selezionare eventi sovrastimati, E (previsione | osservazione = m) > m.
Previsioni deterministiche: avresti dovuto saperlo, sempre!
Perché questo ci lascia perplessi? Perché ci sentiamo a disagio con questa discrepanza tra l'osservazione media e la previsione media? La nostra intuizione si basa sull'uguaglianza di previsione e osservazione che caratterizza le previsioni deterministiche . Nel linguaggio delle probabilità, una previsione deterministica esprime: P (osservazione = previsione) = 1 e P (osservazione ≠ previsione) = 0
Il previsore crede che l'osservazione corrisponderà esattamente alla sua previsione, cioè i valori previsti e osservati coincidono con la probabilità 1 (o 100%), mentre tutti gli altri risultati sono ritenuti impossibili. Questa è un'affermazione sicura di sé, per non dire audace. Espresso tramite probabilità condizionali, possiamo riassumere:

In parole, ogni volta che prevediamo di vendere K pezzi (la condizione dopo la barra verticale), venderemo K pezzi. Poiché il determinismo non implica solo che ogni volta che prevediamo k osserviamo k, ma anche che ogni osservazione k è stata correttamente prevista ex ante come k, abbiamo:
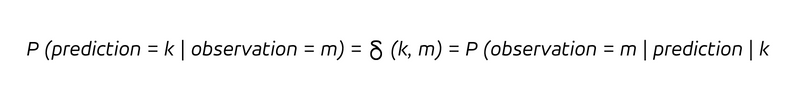
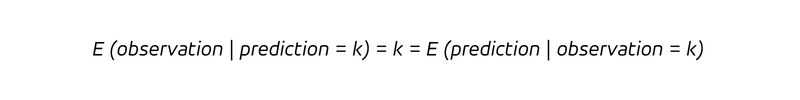
Il determinismo rende obsoleta la distinzione tra le questioni che guardano al passato e quelle che guardano al futuro. Con una previsione deterministica, non impariamo nulla di nuovo osservando il risultato (lo sapevamo già!) e non aggiorneremmo la nostra convinzione (che era già corretta).
Per una tale previsione deterministica, per la quale tutte le distribuzioni di probabilità che appaiono collassano a un picco del 100% all'unico e solo risultato possibile, non si verifica alcun bias di selezione a posteriori: fingiamo di averlo saputo esattamente in anticipo, quindi avremmo dovuto saperlo, sempre e in tutte le circostanze. Se la misurazione dice il contrario, la tua previsione "deterministica" è sbagliata.
Ogni previsione seria è probabilistica
Le previsioni probabilistiche fanno affermazioni più deboli di quelle deterministiche, e per le previsioni probabilistiche dobbiamo abbandonare l'idea che ogni risultato m sia stato previsto in media m - le previsioni deterministiche sembrano quindi molto attraenti. Ma è realistico prevedere le vendite giornaliere di magliette in modo deterministico? Supponiamo che tu sia stato in grado di farlo e prevediamo che le vendite di magliette di domani saranno 5. Ciò significa che puoi nominare cinque persone che, qualunque cosa accada (incidente, malattia, temporale, improvviso cambiamento di idea...) compreranno una maglietta rossa domani. Come possiamo aspettarci di raggiungere un tale livello di certezza? Sei mai stato così sicuro che avresti comprato una maglietta rossa il giorno dopo? Anche se cinque amici hanno promesso che avrebbero comprato una maglietta domani in ogni circostanza, come si potrebbe escludere che qualcun altro, tra tutti gli altri potenziali clienti, comprerebbe anche una maglietta? A parte alcuni casi limite molto idiosincratici (pochissimi clienti, il livello delle scorte è molto più piccolo della domanda reale), prevedere il numero esatto di vendite di un articolo in modo deterministico è fuori discussione. L'incertezza può essere domata solo fino a un certo punto e qualsiasi previsione realistica è probabilistica.
Valutazione igiene
C'è un modo alternativo per confutare la tabella 1: impostando la tabella, poniamo una domanda statistica, vale a dire se la previsione è distorta o meno, e in quale direzione (ignoriamo la questione della significatività statistica per il momento e assumiamo che ogni segnale che vediamo sia statisticamente significativo). Proprio come qualsiasi analisi statistica, un'analisi previsionale può soffrire di distorsioni. Il modo in cui abbiamo selezionato in base ai risultati è un ottimo esempio per il bias di selezione: gli eventi nel gruppo "venditori lenti", "venditori medi", "venditori veloci" non sono rappresentativi dell'intero insieme di previsioni e osservazioni, ma li abbiamo raggruppati in quelli sottostimati e sovrastimati. Inoltre, nella valutazione previsionale abbiamo utilizzato quelle che vengono chiamate "informazioni future": i bucket in cui abbiamo raggruppato le previsioni e le osservazioni non sono ancora definiti al momento della previsione, ma sono stabiliti ex post. Pertanto, impostare la tabella come abbiamo fatto noi viola i principi di base per le analisi statistiche.
Regressione alla media
Il fenomeno che abbiamo appena incontrato – non si prevedeva che gli eventi estremi fossero così estremi come si sono rivelati – è direttamente correlato alla "regressione alla media", un fenomeno statistico per il quale non abbiamo nemmeno bisogno di una previsione: supponiamo di osservare una serie temporale di vendite di un prodotto che non mostra stagionalità o altri modelli dipendenti dal tempo. Quando, in un dato giorno, le vendite osservate sono superiori alle vendite medie, possiamo essere abbastanza sicuri che l'osservazione del giorno successivo sarà inferiore a quella di oggi, e viceversa. Anche in questo caso, selezionando un valore molto grande o molto piccolo, a causa della natura probabilistica del processo, è probabile che selezioniamo una fluttuazione casuale positiva o negativa e le vendite alla fine "regrediranno alla media". Psicologicamente, siamo inclini ad attribuire causalmente tale regressione alla media – un fenomeno puramente statistico – a qualche intervento attivo.
Soluzione: raggruppa per previsione, non per risultato. Rimani vigile contro i pregiudizi di selezione.
Qual è la via d'uscita da questo enigma? Raggruppando per risultati, selezioniamo valori "piuttosto grandi" o "piuttosto piccoli" rispetto alla loro previsione: non stiamo ottenendo un campione rappresentativo, ma distorto. Questo bias di selezione porta a bucket che contengono risultati che sono naturalmente rispettivamente "piuttosto sottostimati" o "piuttosto sovrastimati". Soffriamo del bias di selezione del senno di poi se crediamo che la previsione media e l'osservazione media debbano essere le stesse all'interno degli elementi in movimento "lento", "medio" e "veloce". Dobbiamo convivere e accettare la discrepanza tra le due colonne. Fortunatamente, possiamo usare il teorema di Bayes per ottenere il valore di aspettativa realistico. Una soluzione è quindi un'altra colonna della tabella che contiene il valore teoricamente previsto della previsione media per bucket, che può essere confrontato con la previsione media effettiva in quel bucket. Cioè, possiamo quantificare e riprodurre teoricamente il bias di selezione a posteriori e vedere se i dati aggregati corrispondono alle aspettative teoriche.
Una soluzione molto più semplice, però, è quella di porre domande diverse ai dati, ovvero domande che siano allineate con ciò che la previsione ci promette. Questo ci permette di verificare direttamente se queste promesse sono state mantenute o meno: invece di raggruppare per bucket di risultati, raggruppiamo per bucket di previsione, cioè per venditori lenti, medi e veloci previsti . Qui, possiamo verificare se la promessa della previsione (le vendite medie date una certa previsione corrispondono a quella previsione) è stata mantenuta. Per il nostro esempio, otteniamo questa tabella:
| Frequenza di vendita prevista | Vendite medie osservate | Previsione media |
| Lento <3 pezzi/giorno | 1.288 | 1.267 |
| Medio 3 pezzi/giorno | 5.247 | 5.229 |
| Veloce >3 pezzi/giorno | 12.855 | 12.950 |
Tenendo conto del numero totale di misurazioni, un test di significatività statistica sarebbe negativo, cioè non mostrerebbe alcuna differenza significativa tra la media delle vendite osservate e la previsione media. Concluderemmo che la nostra previsione non è solo imparziale a livello globale, ma anche imparziale per strato di previsione.
In generale, è possibile valutare una previsione filtrando tutte le informazioni note al momento della previsione e la previsione deve essere imparziale in tutti i test. Tuttavia, il filtro non può contenere informazioni future come le fluttuazioni casuali che si verificano nelle osservazioni, su cui la natura decide solo nel futuro del punto di previsione nel tempo.
Cosa dovresti portare via se sei arrivato a questo punto? (1) Quando si seleziona in base al risultato, non si dispone di un campione rappresentativo. (2) Sii scettico nei confronti delle tue aspettative: le aspettative intuitive dall'aspetto molto ragionevole si rivelano imperfette. (3) Rendi esplicite le tue aspettative e mettile alla prova con casi ben compresi.













